Graph with even degree
WebThe end behavior of a polynomial function is the behavior of the graph of f ( x) as x approaches positive infinity or negative infinity. The degree and the leading coefficient of a polynomial function determine the end behavior of the graph. The leading coefficient is significant compared to the other coefficients in the function for the very ... The construction of such a graph is straightforward: connect vertices with odd degrees in pairs (forming a matching), and fill out the remaining even degree counts by self-loops. The question of whether a given degree sequence can be realized by a simple graph is more challenging. See more In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for the two ends of the edge. The degree … See more The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a See more • If each vertex of the graph has the same degree k, the graph is called a k-regular graph and the graph itself is said to have degree k. Similarly, a bipartite graph in which every two vertices on the same side of the bipartition as each other have the same degree is … See more The degree sum formula states that, given a graph $${\displaystyle G=(V,E)}$$, $${\displaystyle \sum _{v\in V}\deg(v)=2 E \,}$$. The formula implies that in any undirected graph, the number of vertices with odd degree is even. … See more • A vertex with degree 0 is called an isolated vertex. • A vertex with degree 1 is called a leaf vertex or end vertex or a pendant vertex, and the edge incident with that vertex is called … See more • Indegree, outdegree for digraphs • Degree distribution • Degree sequence for bipartite graphs See more
Graph with even degree
Did you know?
WebJul 17, 2024 · The graph shown above has an Euler circuit since each vertex in the entire graph is even degree. Thus, start at one even vertex, travel over each vertex once and … WebAug 16, 2024 · An undirected graph has an Eulerian path if and only if it is connected and has either zero or two vertices with an odd degree. If no vertex has an odd degree, then the graph is Eulerian. Proof. It can be proven by induction that the number of vertices in an undirected graph that have an odd degree must be even.
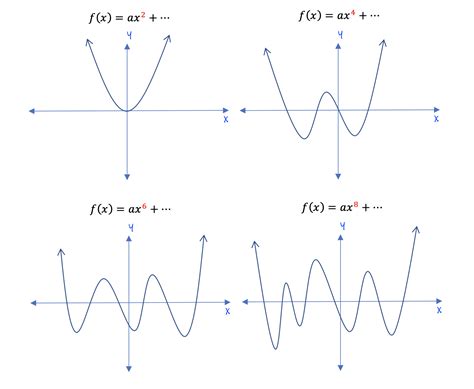
WebDec 21, 2024 · If the function is odd, the graph is symmetrical about the origin. Even function: The mathematical definition of an even function is f (– x) = f ( x) for any value … WebA constant, C, counts as an even power of x, since C = Cx^0 and zero is an even number. So in this case you have x^5: (odd) x^3: (odd) ... you're going to get an even function. It's made up of a bunch of terms that all have even degrees. So it's the sixth degree, fourth degree, second degree; you could view this as a zero'th degree right over ...
Web30K views 6 years ago This MATHguide math education video demonstrates the connection between leading terms, even/odd degree, and the end behavior of polynomials. [Tagalog] Write Polynomial... WebSep 29, 2024 · Definitions: Euler Paths and Circuits. A graph has an Euler circuit if and only if the degree of every vertex is even. A graph has an Euler path if and only if there are at most two vertices with odd degree. Since the bridges of Königsberg graph has all four vertices with odd degree, there is no Euler path through the graph.
In graph theory, an Eulerian trail (or Eulerian path) is a trail in a finite graph that visits every edge exactly once (allowing for revisiting vertices). Similarly, an Eulerian circuit or Eulerian cycle is an Eulerian trail that starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. The problem can be sta…
WebApr 11, 2016 · Second way. Imagine you are drawing the graph. First, you draw all vertices. Since there are not yet any edges, every vertex, as of now, has degree 0, which clearly is even. Therefore there are zero nodes of odd degree, which, again, is an even number. Then you add the edges, one at a time. For each edge, one of the following can happen: inability to pee medical termhttp://phd.big-data-fr.com/wp-content/uploads/2015/11/kjohd6u4/which-graph-shows-a-polynomial-function-of-an-even-degree%3F inability to perch wellWebEuler Graph Example- The following graph is an example of an Euler graph- Here, This graph is a connected graph and all its vertices are of even degree. Therefore, it is an Euler graph. Alternatively, the above … inability to perceive one or more colorsWebLearn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for … inability to performWebThe exponent says that this is a degree- 4 polynomial; 4 is even, so the graph will behave roughly like a quadratic; namely, its graph will either be up on both ends or else be down on both ends. Since the sign on the … in a high pressure system airWebEvery vertex has an even degree, and; All of its vertices with a non-zero degree belong to a single connected component. For example, the following graph has an Eulerian cycle since every vertex has an even degree: 3. Semi–Eulerian. A graph that has an Eulerian trail but not an Eulerian circuit is called Semi–Eulerian. in a high power distanceWebMay 19, 2024 · About 50 years ago, mathematicians predicted that for graphs of a given size, there is always a subgraph with all odd degree containing at least a constant proportion of the total number of vertices in the overall graph — like \frac {1} {2}, or \frac {1} {8}, or \frac {32} {1,007}. Whether a graph has 20 vertices or 20 trillion, the size of ... inability to perform contract